The easy answer seemed to be using OpenCV's cv::solvePnP() (or its C equivalent, cvFindExtrinsicCameraParams2()) by inputting four corners of the detected object calculated from the homography. But I'm getting weird memory errors with this function for some reason ("incorrect checksum for freed object - object was probably modified after being freed.
*** set a breakpoint in malloc_error_break to debug but setting a breakpoint on malloc_error_break didn't really help, and it isn't an Objective-C object giving me trouble, so NSZombiesEnabled won't be any help, etc etc arghhh....) AND it looks like it's possible to decompose a homography matrix into rotation and translation vectors which is all I really need (as long as I have the camera intrinsic matrix, which I found in the last post). solvePnP looks useful if I wanted to do pose estimation from a 3D structure, but I'm sticking to planes for now as a first step. OpenCV's solvePnP() doesn't look like it has an option to use RANSAC which seems important if many points are likely to be outliers-- an assumption that the Ferns-based matcher relies upon.
Now to figure out the homography decomposition... There are some equations here and some code here. I wish this were built into OpenCV. I will update as I find out more.
Update 1: The code found here was helpful. I translated it to C++ and used the OpenCV matrix libraries, so it required a little more work than a copy-and-paste. The 3x3 rotation matrix it produces is made up of the three orthogonal vectors that OpenGL wants (so they imply a rotation, but they're not three Euler angles or anything) which this image shows nicely:
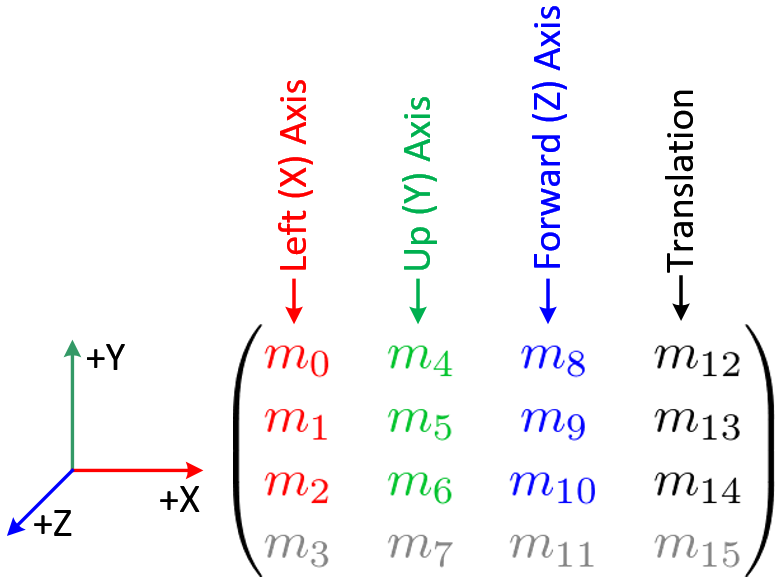 |
| Breakdown of the OpenGL modelview matrix (via) |
The translation vector seems to be translating correctly as I move the camera around, but I'm not sure how it's scaled. Values seem to be in the +/- 1.0 range, so maybe they are in screen widths? Certainly they aren't pixels. Maybe if I actually understood what was going on I'd know better... Well, time to set up OpenGL ES rendering and try this out.
Update 2: Forgot for a minute that OpenGL's fixed pipeline requires two transformation matrices: a modelview matrix (which I figure out above, based on the camera's EXtrinsic properties) and a projection matrix (which is based on the camera's INtrinsic properties). These resources might be helpful in getting the projection matrix.
Update 3: Ok, got it figured out. It's not pretty, but it works. I think I came across the same thing as this guy. Basically I needed to switch the sign on four out of nine elements of the modelview rotation matrix and two of the three components of the translation vector. The magnitudes were correct, but it was rotating backwards in the z-axis and translating backwards in the x- and y- axes. This was extremely frustrating. So, I hope the code after the jump helps someone else out...
// Transform the camera's intrinsic parameters into an OpenGL camera matrix glMatrixMode(GL_PROJECTION); glLoadIdentity(); // Camera parameters double f_x = 786.42938232; // Focal length in x axis double f_y = 786.42938232; // Focal length in y axis (usually the same?) double c_x = 217.01358032; // Camera primary point x double c_y = 311.25384521; // Camera primary point y double screen_width = 480; // In pixels double screen_height = 640; // In pixels double fovY = 1/(f_x/screen_height * 2); double aspectRatio = screen_width/screen_height * f_y/f_x; double near = .1; // Near clipping distance double far = 1000; // Far clipping distance double frustum_height = near * fovY; double frustum_width = frustum_height * aspectRatio; double offset_x = (screen_width/2 - c_x)/screen_width * frustum_width * 2; double offset_y = (screen_height/2 - c_y)/screen_height * frustum_height * 2; // Build and apply the projection matrix glFrustumf(-frustum_width - offset_x, frustum_width - offset_x, -frustum_height - offset_y, frustum_height - offset_y, near, far);
// Decompose the Homography into translation and rotation vectors // Based on: https://gist.github.com/740979/97f54a63eb5f61f8f2eb578d60eb44839556ff3f Mat inverseCameraMatrix = (Mat_(3,3) << 1/cameraMatrix.at (0,0) , 0 , -cameraMatrix.at (0,2)/cameraMatrix.at (0,0) , 0 , 1/cameraMatrix.at (1,1) , -cameraMatrix.at (1,2)/cameraMatrix.at (1,1) , 0 , 0 , 1); // Column vectors of homography Mat h1 = (Mat_ (3,1) << H_matrix.at (0,0) , H_matrix.at (1,0) , H_matrix.at (2,0)); Mat h2 = (Mat_ (3,1) << H_matrix.at (0,1) , H_matrix.at (1,1) , H_matrix.at (2,1)); Mat h3 = (Mat_ (3,1) << H_matrix.at (0,2) , H_matrix.at (1,2) , H_matrix.at (2,2)); Mat inverseH1 = inverseCameraMatrix * h1; // Calculate a length, for normalizing double lambda = sqrt(h1.at (0,0)*h1.at (0,0) + h1.at (1,0)*h1.at (1,0) + h1.at (2,0)*h1.at (2,0)); Mat rotationMatrix; if(lambda != 0) { lambda = 1/lambda; // Normalize inverseCameraMatrix inverseCameraMatrix.at (0,0) *= lambda; inverseCameraMatrix.at (1,0) *= lambda; inverseCameraMatrix.at (2,0) *= lambda; inverseCameraMatrix.at (0,1) *= lambda; inverseCameraMatrix.at (1,1) *= lambda; inverseCameraMatrix.at (2,1) *= lambda; inverseCameraMatrix.at (0,2) *= lambda; inverseCameraMatrix.at (1,2) *= lambda; inverseCameraMatrix.at (2,2) *= lambda; // Column vectors of rotation matrix Mat r1 = inverseCameraMatrix * h1; Mat r2 = inverseCameraMatrix * h2; Mat r3 = r1.cross(r2); // Orthogonal to r1 and r2 // Put rotation columns into rotation matrix... with some unexplained sign changes rotationMatrix = (Mat_ (3,3) << r1.at (0,0) , -r2.at (0,0) , -r3.at (0,0) , -r1.at (1,0) , r2.at (1,0) , r3.at (1,0) , -r1.at (2,0) , r2.at (2,0) , r3.at (2,0)); // Translation vector T translationVector = inverseCameraMatrix * h3; translationVector.at (0,0) *= 1; translationVector.at (1,0) *= -1; translationVector.at (2,0) *= -1; SVD decomposed(rotationMatrix); // I don't really know what this does. But it works. rotationMatrix = decomposed.u * decomposed.vt; } else { printf("Lambda was 0...\n"); } modelviewMatrix = (Mat_ (4,4) << rotationMatrix.at (0,0), rotationMatrix.at (0,1), rotationMatrix.at (0,2), translationVector.at (0,0), rotationMatrix.at (1,0), rotationMatrix.at (1,1), rotationMatrix.at (1,2), translationVector.at (1,0), rotationMatrix.at (2,0), rotationMatrix.at (2,1), rotationMatrix.at (2,2), translationVector.at (2,0), 0,0,0,1);
'Camera Calibration' 카테고리의 다른 글
| Camera calibration With OpenCV (0) | 2013.03.22 |
|---|---|
| Cholesky decomposition을 이용한 카메라 행렬 분해 (1) | 2013.03.22 |
| Step by Step Camera Pose Estimation for Visual Tracking and Planar Markers (0) | 2013.03.22 |
| Homography to camera pose(extrinsic) (0) | 2013.03.21 |
| Camera Tracking - Tukey biweight estimator (0) | 2013.03.18 |